B树(B-Tree)详解 - 为什么每个数据库都在使用它
- Published on
为什么需要B树?
问题的起源
storage/innobase/btr/btr0cur.cc
btr_page_split_and_insert() in btr_cur_pessimistic_insert() invokes...
悲观插入,这是当节点太满时的代码路径,当乐观插入失败时,当你必须分裂时。
我跟着函数找到btr0btr.cc。数百行C代码、分裂条件、溢出保护、还有一个我没有的边界检查。
我滚动查看我的Python代码:
if len(node.keys) >= self.order: # 没有-1
self._split_child(parent, index)
书里已经警告过这一点。第263页:"如果一个节点最多能容纳N个键值对,再插入一个就超过了它的最大容量N。"
超过,不是等于,是超过!
B树的设计思想
核心思想
B树是一种自平衡树,专为磁盘访问优化。与二叉搜索树(每个节点只有2个子节点)不同,B树的每个节点有成百上千个子节点。
关键思想:每个B树节点都装入一个磁盘块(4KB到16KB)。既然我们必须读取整个块,那就尽可能多地打包键值对。
为什么这样设计是高效的?
二进制特性:
- 任何正整数都可以表示为若干个2的幂的和
- 这种特性使得我们可以用O(log n)个节点表示任意区间
区间管理:
- 每个节点管理的区间长度是2的幂
- 这种设计使得更新和查询操作都非常高效
二叉搜索树在磁盘上的问题
让我们先从不适合的方法开始:二叉搜索树(BST)在磁盘上。
在内存中,二叉搜索树非常出色。每个节点存储一个键值,有两个子节点(左和右)。左子树中的键值较小,右子树中的键值较大。找到一个键值需要O(log₂ n)次比较。
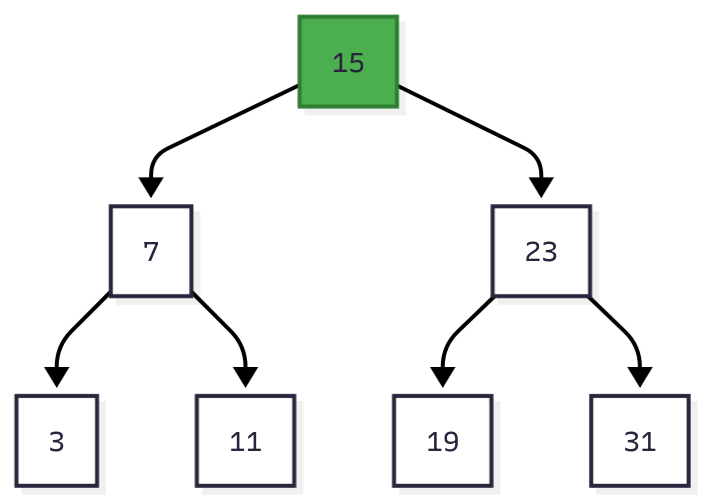
图1:有7个节点的二叉搜索树。查找键值11需要3次比较:15 → 7 → 11。
对于100万条记录,平衡的BST高度为log₂(1,000,000) ≈ 20。也就是说,找到任何记录需要20次比较。
在内存中,这很快。 每次比较是指针解引用(现代CPU上约0.0001毫秒)。总查找时间:0.002毫秒。
在磁盘上,这是灾难性的。 原因如下:
磁盘I/O很昂贵
磁盘访问的最小单位是块(通常是4KB到16KB)。要从磁盘读取单个字节,你必须读取包含它的整个块。
磁盘访问时间:
- RAM访问:0.0001毫秒
- SSD访问:0.1毫秒
- HDD访问:10毫秒
- 磁盘比RAM慢100-100,000倍
二叉树的灾难
在磁盘上使用BST时,每个节点存储在单独的磁盘块中。从父节点遍历到子节点需要磁盘寻道。
对于100万条记录:
- 高度:20个节点
- 磁盘寻道:20次
- HDD上时间:20 × 10毫秒 = 200毫秒
- SSD上时间:20 × 0.1毫秒 = 2毫秒
对于SSD来说还可以接受,但对HDD来说太糟糕了。随着树的增长,情况会变得更糟。
对于10亿条记录:
- 高度:30个节点
- HDD上时间:30 × 10毫秒 = 300毫秒
- SSD上时间:30 × 0.1毫秒 = 3毫秒
根本问题: BST的扇出太低(每个节点只有2个子节点)。我们需要每个节点有更多的子节点来减少树的高度。
为什么不直接平衡树?
你可能会想:"直接保持树的平衡!" 红黑树和AVL树就是这样做的。
问题不只是树的高度——还有维护成本。平衡需要旋转节点和更新指针。在内存中,这很便宜(几次指针写入)。在磁盘上,这很昂贵:
- 从磁盘读取节点(4KB块)
- 在内存中修改节点
- 将修改后的节点写回磁盘(4KB块)
- 更新父指针(更多磁盘I/O)
对于频繁插入和删除的树,不断的重新平衡会扼杀性能。我们需要一个:
- 具有高扇出(每个节点有多个子节点)→ 减少高度
- 需要很少的重新平衡 → 减少I/O开销
的数据结构。
那个数据结构就是B树。
什么是B树?
B树结构
B树是自平衡树,为磁盘访问优化。与2个子节点的二叉树不同,B树节点有成百上千个子节点。
关键思想: 每个B树节点装入一个磁盘块(4KB到16KB)。既然我们必须读取整个块,那就尽可能多地打包键值对。
B树结构
B树节点存储:
- N个键值(排序的)
- N + 1个指针 指向子节点
每个键值充当分隔符:child[i]中的键值 < key[i] < child[i+1]中的键值。
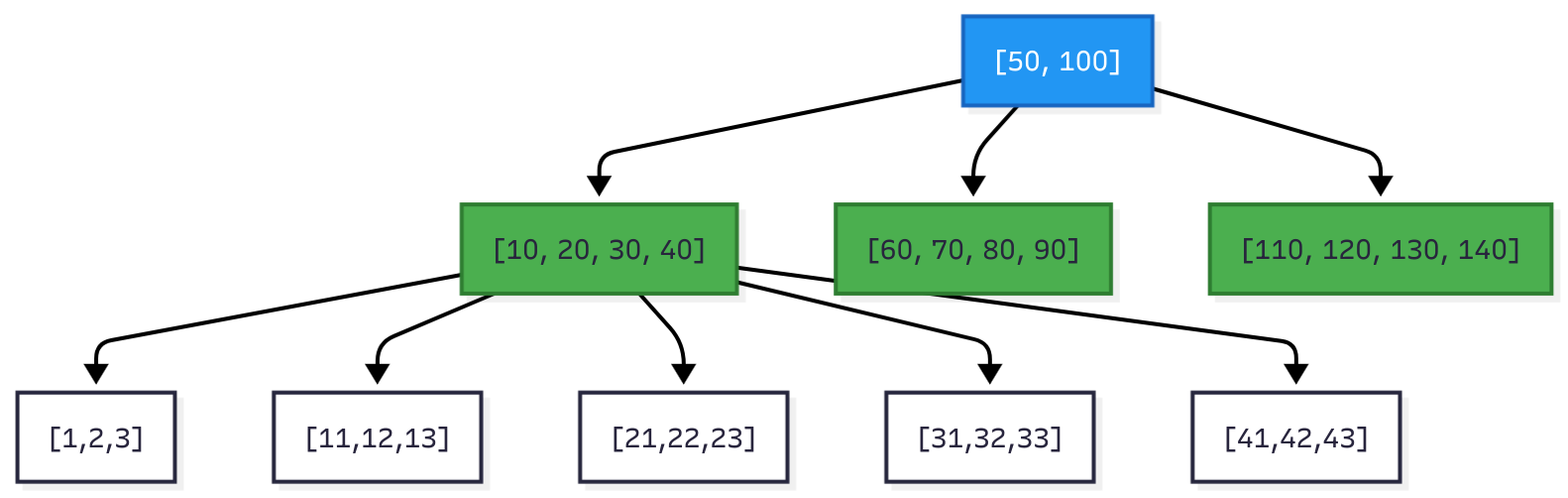
图2:扇出约100的B树。根节点有2个键和3个子节点。内部节点有4个键和5个子节点。叶子节点包含实际数据。
B树层次结构
B树有三种类型的节点:
根节点: 树的顶部。总只有一个根。
内部节点: 指导搜索的中间层。它们存储分隔键和指针,但不存储实际数据。
叶子节点: 包含实际数据(键值对)的底层。所有叶子都在同一深度。
这是B+树(最常见的变种)。B+树只在叶子存储数据,而B树也可以在内部节点存储数据。每个主流数据库都使用B+树,但为了简单称之为"B树"。
为什么高扇出很重要
二叉树(扇出 = 2):
- 100万记录 → 高度 = 20
- 10亿记录 → 高度 = 30
B树(扇出 = 100):
- 100万记录 → 高度 = 3(因为100³ = 1,000,000)
- 10亿记录 → 高度 = 5(因为100⁵ = 10,000,000,000)
B树(扇出 = 1000):
- 100万记录 → 高度 = 2(因为1000² = 1,000,000)
- 10亿记录 → 高度 = 3(因为1000³ = 1,000,000,000)
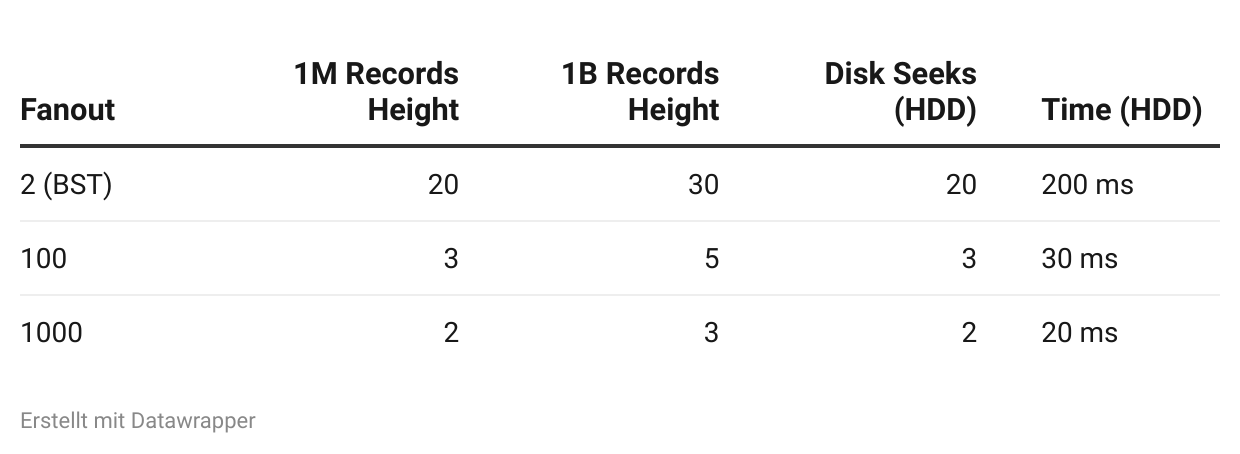
高扇出 = 更少的磁盘寻道 = 更快的查询。
B树查找算法
在B树中查找键值是从根到叶子的遍历,在每个节点进行二分查找。
算法:
- 从根节点开始
- 在当前节点内二分查找键值,找到分隔键值范围
- 跟随相应的子节点指针
- 重复直到到达叶子节点
- 在叶子中,要么找到键值,要么得出不存在的结论
时间复杂度:
- 树高度:O(log_fanout n)
- 每个节点二分查找:O(log₂ fanout)
- 总计:O(log n)
示例: 在扇出100、100万记录的B树中查找键值72。
步骤1:读取根节点(1次磁盘I/O)
键值:[50, 100, 150, ...]
72在50和100之间
跟随子节点指针2
步骤2:读取内部节点(1次磁盘I/O)
键值:[55, 60, 65, 70, 75, 80, ...]
72在70和75之间
跟随子节点指针5
步骤3:读取叶子节点(1次磁盘I/O)
键值:[71, 72, 73, 74]
找到!返回键值72的值
总计:3次磁盘I/O操作 = HDD上30毫秒,SSD上0.3毫秒
Python中的工作实现
让我们用Python实现一个简化但功能完整的B树。
from typing import List, Optional
from dataclasses import dataclass, field
@dataclass
class BTreeNode:
"""
B树节点,存储键值和子节点指针。
属性:
keys: 该节点中排序后的键值列表
children: 子节点指针列表(长度 = len(keys) + 1)
is_leaf: 是否为叶子节点(无子节点)
不变量:
- len(children) == len(keys) + 1(对于内部节点)
- 所有键值都是排序的
- children[i]中的键 < keys[i] < children[i+1]中的键
"""
keys: List[int] = field(default_factory=list)
children: List['BTreeNode'] = field(default_factory=list)
is_leaf: bool = True
def __repr__(self):
return f"BTreeNode(keys={self.keys}, is_leaf={self.is_leaf})"
class BTree:
"""
B树实现,可配置阶数(最大子节点数)。
属性:
order: 每个节点的最大子节点数(扇出)
root: 树的根节点
属性:
- 每个节点最多有 (order - 1) 个键
- 每个非根节点至少有 (order // 2 - 1) 个键
- 树高度是 O(log_order n)
时间复杂度:
- 查找: O(log n)
- 插入: O(log n)
- 删除: O(log n)
空间复杂度: O(n)
"""
def __init__(self, order: int = 100):
"""
初始化B树。
参数:
order: 每个节点的最大子节点数(扇出)。
更高的阶数 = 更少的层数但更大的节点。
基于磁盘存储的典型值:100-1000。
"""
if order < 3:
raise ValueError("阶数必须至少为3")
self.order = order
self.root = BTreeNode()
def search(self, key: int) -> Optional[int]:
"""
在B树中搜索键值。
参数:
key: 要搜索的键值
返回:
如果找到返回键值,否则返回None
时间复杂度: O(log n),n为键的数量
"""
return self._search_recursive(self.root, key)
def _search_recursive(self, node: BTreeNode, key: int) -> Optional[int]:
"""
从节点开始递归搜索键值。
使用节点内的二分查找找到正确的子节点。
"""
# 节点内二分查找
i = self._binary_search(node.keys, key)
# 找到精确匹配
if i < len(node.keys) and node.keys[i] == key:
return key
# 到达叶子节点但未找到
if node.is_leaf:
return None
# 递归到适当的子节点
# (实际实现中,这会是磁盘I/O)
return self._search_recursive(node.children[i], key)
def _binary_search(self, keys: List[int], key: int) -> int:
"""
二分查找键值的插入位置。
返回:
索引i,使得keys[i-1] < key <= keys[i]
时间复杂度: O(log m),m为节点中的键数量
"""
left, right = 0, len(keys)
while left < right:
mid = (left + right) // 2
if keys[mid] < key:
left = mid + 1
else:
right = mid
return left
def insert(self, key: int):
"""
向B树插入键值。
参数:
key: 要插入的键值
时间复杂度: O(log n)
算法:
1. 找到合适的叶子节点
2. 将键值插入叶子
3. 如果叶子溢出(键值太多),分裂它
4. 如果需要,将分裂向上传播
"""
root = self.root
# 如果根节点满了,分裂它并创建新根
if len(root.keys) >= self.order - 1:
new_root = BTreeNode(is_leaf=False)
new_root.children.append(self.root)
self._split_child(new_root, 0)
self.root = new_root
self._insert_non_full(self.root, key)
def _insert_non_full(self, node: BTreeNode, key: int):
"""
向未满的节点插入键值。
递归地找到正确的叶子节点并插入。
"""
i = len(node.keys) - 1
if node.is_leaf:
# 插入到排序位置
node.keys.append(None) # 腾出空间
while i >= 0 and key < node.keys[i]:
node.keys[i + 1] = node.keys[i]
i -= 1
node.keys[i + 1] = key
else:
# 找到要插入的子节点
while i >= 0 and key < node.keys[i]:
i -= 1
i += 1
# 如果子节点满了,先分裂它
if len(node.children[i].keys) >= self.order - 1:
self._split_child(node, i)
if key > node.keys[i]:
i += 1
self._insert_non_full(node.children[i], key)
def _split_child(self, parent: BTreeNode, child_index: int):
"""
分裂满的子节点为两个节点。
参数:
parent: 包含满子节点的父节点
child_index: 满子节点在父节点children中的索引
算法:
1. 创建新的兄弟节点
2. 将满子节点的一半键值移动到兄弟节点
3. 将中间键值提升到父节点
4. 更新父节点的子节点列表
"""
full_child = parent.children[child_index]
new_sibling = BTreeNode(is_leaf=full_child.is_leaf)
mid = (self.order - 1) // 2
# 将一半键值移动到新兄弟节点
new_sibling.keys = full_child.keys[mid + 1:]
full_child.keys = full_child.keys[:mid]
# 如果不是叶子节点,移动一半子节点
if not full_child.is_leaf:
new_sibling.children = full_child.children[mid + 1:]
full_child.children = full_child.children[:mid + 1]
# 将中间键值提升到父节点
promoted_key = full_child.keys[mid]
parent.keys.insert(child_index, promoted_key)
parent.children.insert(child_index + 1, new_sibling)
def print_tree(self, node: Optional[BTreeNode] = None, level: int = 0):
"""
打印树结构用于调试。
"""
if node is None:
node = self.root
print(" " * level + f"Level {level}: {node.keys}")
if not node.is_leaf:
for child in node.children:
self.print_tree(child, level + 1)
# 使用示例
if __name__ == "__main__":
# 创建阶数为5的B树(每个节点最多4个键)
btree = BTree(order=5)
# 插入键值
keys = [10, 20, 5, 6, 12, 30, 7, 17, 3, 16, 21, 24, 25, 26, 27]
print("插入键值:", keys)
for key in keys:
btree.insert(key)
print("\nB树结构:")
btree.print_tree()
# 搜索键值
print("\n搜索键值:")
for search_key in [6, 16, 21, 100]:
result = btree.search(search_key)
if result:
print(f" 键 {search_key}: 找到")
else:
print(f" 键 {search_key}: 未找到")
输出:
插入键值: [10, 20, 5, 6, 12, 30, 7, 17, 3, 16, 21, 24, 25, 26, 27]
B树结构:
Level 0: [12, 20, 25]
Level 1: [3, 5, 6, 7, 10]
Level 1: [16, 17]
Level 1: [21, 24]
Level 1: [26, 27, 30]
搜索键值:
键 6: 找到
键 16: 找到
键 21: 找到
键 100: 未找到
为什么这个实现有效:
- 每个节点存储最多
order - 1个键 - 分裂操作维护B树的不变量
- 节点内二分查找减少比较
- 树高度保持对数
B树节点分裂
当你向满的叶子节点插入键值时,节点必须分裂。
分裂算法:
- 找到满节点的中点
- 创建新的兄弟节点
- 将一半键值移动到新节点
- 将中间键值提升到父节点
- 如果父节点满了,递归地分裂它
当分裂传播到根节点时:
- 根节点分裂为两个节点
- 创建新根节点,包含一个键值(从旧根提升的)
- 树高增加1
这是B树高度增加的唯一方式。B树从叶子向上生长,而不是从根向下生长。
B树的性能特征
查找复杂度
时间复杂度:O(log n)
对于n个键值、扇出f的树:
- 树高度:log_f(n)
- 每个节点二分查找:log₂(f)
- 总比较次数:log_f(n) × log₂(f) = O(log n)
磁盘I/O:log_f(n) 次磁盘读取(每层一次)
插入复杂度
时间复杂度:O(log n)
- 查找插入位置:O(log n)
- 插入到叶子:O(f) 移动键值
- 必要时分裂:O(f) 移动键值
- 分裂向上传播:最坏情况O(log n) 层
磁盘I/O:O(log n) 次磁盘读取 + O(log n) 次磁盘写入
删除复杂度
时间复杂度:O(log n)
- 查找键值:O(log n)
- 从叶子删除:O(f) 移动键值
- 必要时合并:O(f) 移动键值
- 合并向上传播:最坏情况O(log n) 层
磁盘I/O:O(log n) 次磁盘读取 + O(log n) 次磁盘写入
空间复杂度
空间:O(n)
每个键值存储一次。内部节点增加开销(指针和分隔键),但这通常是数据大小的10-20%。
占用率:节点通常是50-90%满。更高的扇出提高空间效率,因为指针开销成比例地变小。
真实世界的B树应用
每个主要数据库都使用B树(或B+树)作为索引。
MySQL InnoDB
InnoDB使用B+树作为:
- 主键索引(聚簇索引):叶子节点存储实际行数据
- 二级索引:叶子节点存储指向主键的指针
InnoDB B树配置:
- 页大小:16KB(默认)
- 扇出:约100-200,取决于键值大小
- 100万行数据的树高:3-4层
示例:
-- 创建带主键的表
CREATE TABLE users (
id INT PRIMARY KEY,
name VARCHAR(100),
email VARCHAR(100)
) ENGINE=InnoDB;
-- 主键自动创建聚簇B+树索引
-- 叶子节点包含实际行数据
-- 树结构:id=1与name和email一起存储在叶子中
-- 在email上创建二级索引
CREATE INDEX idx_email ON users(email);
-- 二级索引是单独的B+树
-- 叶子节点包含email → id映射
-- 要获取完整行:在idx_email中查找email → 获取id → 查找主键中的id
PostgreSQL
PostgreSQL默认使用B树作为索引类型。
PostgreSQL B树配置:
- 页大小:8KB(默认)
- 扇出:约50-100,取决于键值大小
- 支持多种索引类型,但B树是默认
其他数据库系统
- SQLite:使用B树存储表和索引
- MongoDB WiredTiger:使用B树作为索引
- Oracle、SQL Server:都使用B树的变体
权衡和限制
B树并不完美。以下是它们遇到的困难:
写放大
每次插入都可能触发一直传播到根的分裂。最坏情况下:
- 插入1个键 → 分裂叶子 → 分裂父节点 → 分裂祖父节点 → 分裂根节点
- 1个逻辑写入变成4+个物理写入
示例: 插入100万个键值,频繁分裂:
- 逻辑写入:100万
- 物理写入(带分裂):200-300万
- 写放大:2-3倍
替代方案: LSM树(Log-Structured Merge Trees),被RocksDB、Cassandra使用。
非顺序键值上的范围查询
B树为索引键值上的范围查询进行了优化,但在多列范围查询方面有困难。
示例:
-- 快速:索引列上的范围查询
SELECT * FROM orders WHERE order_date BETWEEN '2024-01-01' AND '2024-12-31';
-- B树顺序遍历叶子节点(叶子节点是链接的)
-- 慢:非索引列上的范围查询
SELECT * FROM orders WHERE total_amount BETWEEN 100 AND 200;
-- 必须扫描整个表(total_amount上没有索引)
缓存的内存开销
为了避免磁盘I/O,数据库在内存中缓存频繁访问的B树节点。对于大型数据库:
- 10亿条记录
- 树高:4层
- 内部节点:约100万个
- 缓存大小:约16GB(缓存所有内部节点)
经验法则:计划数据库大小的10-20%作为RAM用于B树缓存。
随时间推移的碎片化
经过多次插入和删除后,B树节点可能只有50-60%满。这会浪费空间并增加树的高度。
解决方案: 定期VACUUM(PostgreSQL)或OPTIMIZE TABLE(MySQL)来重建B树。
并发挑战
B树在分裂和合并期间需要锁定。在高并发工作负载中,锁争用可能成为写入的瓶颈。
何时不用B树
B树非常适合基于磁盘的排序数据,但并非总是最优选择:
写密集型工作负载
如果你每秒进行100,000次写入而读取很少,LSM树的表现优于B树。
示例:
- B树:MySQL、PostgreSQL、SQLite
- LSM树:RocksDB、Cassandra、LevelDB
内存数据库
如果你的整个数据集适合RAM,B树会增加不必要的复杂性。哈希索引或跳表更简单、更快。
分析型工作负载(OLAP)
对于扫描数百万行的大型分析查询,列式存储(如Parquet、ORC)优于B树。
总结:为什么B树胜出
经过50多年的发展,B树仍然是主导的磁盘数据结构,因为它们:
- 最小化磁盘I/O:高扇出减少树高度
- 自动平衡:分裂和合并保持所有叶子在同一深度
- 支持范围查询:排序的键值和叶子级链接支持高效扫描
- 适用于任何磁盘:对HDD(顺序I/O)和SSD(块级访问)都进行了优化
关键洞见:B树匹配磁盘存储的约束。由于最小的I/O单位是块,B树尽可能多地打包数据到每个块中。这个简单的想法——最大化扇出以最小化高度——使数据库变得快速。
参考资料
书籍推荐:
- 《数据库系统内幕》Alex Petrov著(O'Reilly,2019)
- 《计算机程序设计艺术,第3卷:排序与查找(第2版)》Donald E. Knuth著
在线资源:
- MySQL官方文档:InnoDB B树索引
- PostgreSQL官方文档:B树索引
- SQLite文档:B树模块
每当查询数据库并在毫秒内得到结果时,都要感谢B树。